모델 검증과 평가 (Validation & Evaluation)
01 May 2020 | Machine-Learning
본 포스트는 문일철 교수님의 인공지능 및 기계학습 개론 I 를 바탕으로 작성하였습니다.
Validation
가지고 있는 데이터셋을 학습 데이터와 테스트 데이터로 왜 나누어야 하는 지를 설명했을 때 나왔던 수험생을 다시 데려와 봅시다. 이전 게시물에서는 수능처럼 학생을 최종적으로 평가하기 위해서 약 20%의 테스트 데이터를 따로 빼두는 과정에 대해 설명하였습니다. 그런데 문제지만 풀다가 수능날 바로 시험을 보는 학생은 많지 않을 것입니다. 자의든 타의든 수능을 대비하기 위한 몇 번의 모의고사를 치르게 됩니다.
모의고사를 치는 이유는 무엇일까요? 수능이 끝나면 그 점수를 그대로 받아야 하는데 그 전에 자기가 부족한 부분은 어디인지, 어떤 상황에서 점수가 좋고 나쁜 지를 판단하기 위해서일 것입니다. 모의고사 결과를 보고 수능 전까지 필요한 부분을 점검하고 보완해나가게 되지요.
머신러닝 모델도 마찬가지입니다. 학습 데이터로 모델을 생성한 뒤에 중간과정 없이 테스트 데이터로 모델을 평가한다고 해봅시다. 이렇게 생성된 모델은 과적합이나 과소적합이 발생할 수 있습니다. 하지만 모델이 우리가 가지고 있는 모든 데이터를 봐버렸기 때문에 이 모델을 개선 후 다시 테스트할 수 있는 방도가 없습니다. 과적합이나 과소적합이 발생하지 않은 모델이라 하더라도 이 모델이 최선인지 더 나은 모델이 있는지 알 수 있는 방법 역시 없게 되지요.
모델에게도 테스트 데이터 전에 자신을 점검해 볼 수 있는 모의고사 같은 과정이 필요합니다. 머신러닝에서는 이를 검증(Validation)이라고 하고 검증에 사용하는 데이터셋을 검증 데이터셋(Validation dataset)이라고 합니다. 검증 데이터셋은 학습 데이터셋의 일부를 사용합니다. 다음으로 다양한 모델 검증 방법에 대해서 알아보겠습니다.
Various Validation
머신러닝 모델의 검증 방법은 크게 3가지로 나눌 수 있습니다. 첫 번째가 Holdout, 두 번째가 K-fold CV, 마지막이 LOOCV입니다. 각각에 대해 알아보도록 합시다.
Holdout
Holdout 검증은 가장 기본적인 모델 검증 방법입니다. 전체 데이터셋에서 테스트 데이터를 분리하고 남은 학습 데이터의 일부를 검증 데이터셋으로 또 분리하는 방법입니다. 즉, 전체 데이터를 3개(학습 데이터, 검증 데이터, 테스트 데이터)로 나누게 되는 것이지요. 이 방식은 가장 간단하지만 학습 데이터에 손실이 있기 때문에 데이터가 적은 경우에 사용하기 힘들고, 검증을 한 번 밖에 진행할 수 없다는 단점이 있습니다. 아래는 홀드아웃 방식을 적용했을 때 데이터가 나누어지는 방식입니다.

이미지 출처 : datavedas.com
K-fold CV
홀드아웃 방식은 학습 데이터에 손실이 있고 검증을 한 번 밖에 할 수 없다는 단점이 있었습니다. 실제로는 이를 개선하기 위한 교차검증(Cross validation, CV) 방식을 사용합니다. 교차 검증은 최소 2번 이상의 검증을 진행하므로 각 검증 결과치의 평균을 모델의 검증 결과로 사용하게 됩니다.
교차 검증의 대표적인 방식으로 K-fold 교차검증(K-fold cross validation)이 있습니다. K-fold 교차 검증은 학습 데이터를 K개로 나눈 뒤 차례대로 하나씩을 검증 데이터셋으로 활용하여 K번 검증을 진행하는 방식입니다. 이 방법도 학습 과정마다 학습 데이터에 손실이 있기는 하지만, 결국 전체 데이터를 다 볼 수 있다는 장점이 있고 검증 횟수를 늘릴 수 있다는 장점도 있습니다. 다음은 $K=5$ 인 K-fold 교차검증이 진행되는 방식을 그림으로 나타낸 것입니다. 일반적으로는 $5 \leq K \leq 11$ 범위의 $K$ 를 설정하여 사용합니다.

이미지 출처 : researchgate.net
LOOCV
LOOCV(Leave-one-out cross validation)는 K-fold 교차 검증의 극단적인 형태로, 학습 데이터셋이 극도로 작을 때 사용할 수 있는 교차검증 방법입니다. LOOCV는 오직 한 개의 인스턴스만을 검증 데이터셋으로 남겨 놓습니다(Leave-one-out). 검증 데이터가 하나이므로 학습 데이터가 총 $N$ 개라면 총 $N$ 번의 교차 검증을 진행하게 됩니다. 학습 데이터의 손실을 최소화 할 수 있지만, 샘플 데이터 수가 1000개만 되어도 총 1000번의 학습과 검증을 진행해야 하기 때문에 시간과 컴퓨팅 자원이 많이 소모된다는 단점이 있습니다. 아래는 LOOCV가 진행되는 방식을 그림으로 나타낸 것입니다.
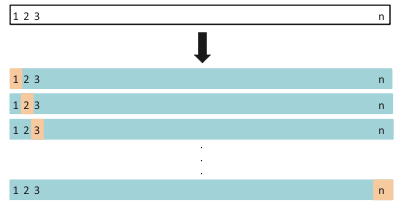
이미지 출처 : smlee729.github.io
아래는 위 3개의 검증 방법을 비교하는 이미지입니다.

이미지 출처 : eda-ai-lab.tistory.com
Hyperparameter Optimization
검증을 통해서 과적합이 일어나는 지점을 찾는 것도 중요하지만, 성능이 좋은 모델을 찾는 것 역시 모델 검증을 해야하는 이유입니다. 더욱 성능이 좋은 모델을 만들기 위해 하이퍼파라미터 최적화를 해주어야 합니다. 하이퍼파라미터(Hyperparameter)는 학습 과정에서 모델이 알아서 바꾸는 파라미터 외에 모델을 만드는 사람이 지정하는 파라미터를 의미합니다. 대표적인 하이퍼파라미터의 예시로는 경사 하강법에서의 학습률(Learning rate), 정칙화(Regulation)의 정도를 조정하는 $\alpha$ 등이 있습니다. 모델마다 설정해주어야 하는 하이퍼파라미터가 다르기 때문에 사용하는 모델에 따라 필요한 하이퍼파라미터를 적당히 조정해주어야 합니다.
어떤 하이퍼파라미터가 최상의 결과를 낳는지 쉽게 알기 어렵고, 하이퍼파라미터의 조합에 따라서도 모델의 결과가 달라지기 때문에 검증 결과를 비교하여 최적의 하이퍼파라미터 조합을 찾아야 합니다. 최적의 하이퍼파라미터 조합을 찾는 방법은 크게 4가지로 나눌 수 있습니다.
Manual Search
말 그대로 수동(Manual)으로 하이퍼파라미터를 조정하는 방식입니다. 모델을 설계하는 사람이 경험에 의한 직관을 사용하여 최적의파라미터 조합을 설정합니다.
Grid Search
하이퍼파라미터마다 적용하고 싶은 값의 목록을 설정해둔 뒤에 그 조합을 모두 시행해보고 최적의 조합을 찾아내는 방식입니다. 직관적으로 이해하기가 쉽지만 조정할 하이퍼 파라미터가많아지면 학습 횟수가 많아지는 단점이 있습니다. 예를 들어, 학습률 $\eta = [0.001, 0.01, 0.1, 1]$ 로 4개, 정칙화 파라미터 $\alpha = [0.001, 0.01, 0.2, 3]$ 로 4개의 목록을 작성한 뒤에 각 조합에 대해 모두 학습을 수행하므로 총 $4 \times 4 = 16$ 번에 대한 학습 및 검증을 하게 됩니다.
Random Search
조정하고 싶은 하이퍼파라미터 마다 조정하고 싶은 범위를 정합니다. 실제 학습 과정에서는 범위 내에 있는 임의의 값을 설정하여 각 파라미터에 대한 조합을 정합니다. Grid search는 지정한 값에 대해서만 학습과 검증을 시도하지만 Random search는 범위 내에 있는 임의의 값에 대하여 예상치 못한 조합을 시도해볼 수 있다는 장점이 있습니다. 아래는 Grid searc h 탐색법과 Random search 탐색법을 비교할 수 있는 이미지입니다.
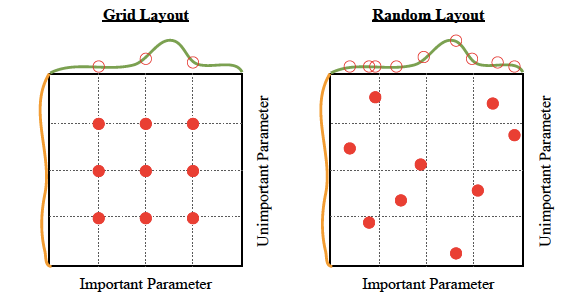
이미지 출처 : nanonets.com
이 3가지 탐색법외에도 베이지안 최적화(Bayesian optimization) 등 다양한 하이퍼파라미터 탐색법이 있습니다. 베이지안 최적화에 대한 자세한 정보는 수아랩(Sualab) 기술블로그에 잘 정리되어 있습니다.
Evaluation
지금부터는 검증(Validation)과 테스트(Test) 단계에서 어떤 지표를 가지고 모델을 평가할 수 있는 지에 대해서 알아보겠습니다.
Confusion Matrix
분류(Classification)에서 가장 많이 사용되는 오차 행렬(Confusion matrix)에 대해서 알아보겠습니다. 오차 행렬은 각 인스턴스의 실제 클래스와 예측 클래스의 개수를 행렬의 성분에 채워넣은 것입니다. 아래 오차 행렬에서는 각 열에 예측 클래스를, 각 행에 실제 클래스를 배치하고 있습니다. (배치는 그리는 사람에 따라 달라질 수 있습니다)
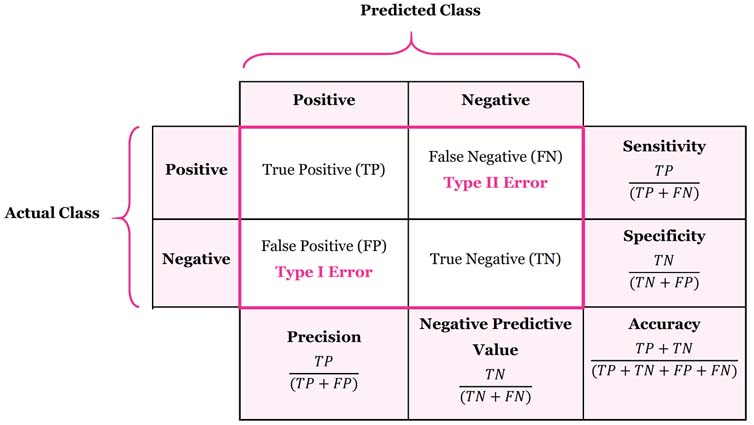
이미지 출처 : manisha-sirsat.blogspot.com
오차 행렬은 2행 2열로 구성되므로 총 4개의 성분이 있습니다. 위 오차 행렬에서 1행 1열의 성분은 True Positive(TP)이며 실제 Positive인 클래스를 Positive로 예측한 인스턴스의 개수를 나타냅니다. 1행 2열의 성분은 False Negative(FN)이며 실제 Positive인 클래스를 Negative로 예측한 인스턴스의 개수를 나타냅니다. 이 때 모델이 잘못 판단한 경우를 Type II Error라고 합니다. 2행 1열의 성분은 False Positive(FP)이며 실제 Negative인 클래스를 Positive로 예측한 인스턴스의 개수를 나타냅니다. 이 때 모델이 잘못 판단한 경우는 Type I Error라고 합니다. 마지막으로 2행 2열의 성분은 True Negative(TN)이며 실제 Negative인 클래스를 Negative로 판단한 인스턴스의 개수를 나타냅니다.
각 이름에 대해서는 “(클래스)로 예측해서 (맞은/틀린) 케이스”으로 기억하면 쉽게 기억할 수 있습니다. 예를 들어, False Positive의 경우는 “(Positive)로 예측해서 (틀린) 케이스”, True Negative는 “(Negative)로 예측해서 (맞은) 케이스” 라고 생각하면 됩니다.
스팸 메일 분류의 예를 들어 보겠습니다. 정상적인 메일을 Negative클래스, 스팸 메일을 Positive클래스라고 하면 TP는 스팸 메일을 스팸 메일로 분류한 경우, FN은 스팸 메일을 정상 메일로 분류한 경우입니다. FP는 정상 메일을 스팸 메일로 분류한 경우이며 TN은 정상적인 메일을 정상 메일로 분류한 경우입니다. 다음은 이 4개의 성분(TP, FN, FP, TN)을 활용한 정확도와 정밀도 및 재현율에 대해 알아보겠습니다.
Accuracy, Precision, Recall
가장 일반적으로 사용되는 것은 정확도(Accuracy)입니다. 정확도는 전체 데이터 중 제대로 판별한(True) 데이터의 비율로, 수치는 다음 수식을 사용하여 구할 수 있습니다.
\[\text{Accuracy} = \frac{\text{TP+TN}}{\text{TP + TN + FP + FN}}\]
데이터셋에서 클래스 비율이 한쪽으로 치우쳐진 경우에는 정확도가 모델의 성능을 제대로 표현하지 못하는 경우도 있습니다. 이런 경우에 대해서는 이후 예시를 통해 알아보겠습니다. 이렇게 정확도가 모델의 제 성능을 표현하지 못하는 경우에는 정밀도와 재현율을 사용합니다. 정밀도(Precision)는 Positive로 예측한 인스턴스 중에 제대로 판별한 비율을 나타냅니다. 재현율(Recall)은 실제 클래스가 Positive인 인스턴스를 얼마나 많이 골라냈는지를 나타내는 수치이며 민감도(Sensitivity)라는 말로도 표현합니다.
\[\begin{aligned}
\text{Precision} &= \frac{\text{TP}}{\text{TP + FP}} \\
\text{Recall} &= \frac{\text{TP}}{\text{TP + FN}}
\end{aligned}\]
위에서 사용했던 스팸 메일의 예를 들어 3개의 수치가 구해지는 과정을 알아보겠습니다. 아래는 총 1000통의 메일 중 스팸메일과 정상 메일을 분류한 예시입니다.
행(실제)/열(예측)
Positive
Negative
Metric
Positive
5(TP)
45(FN)
0.1(Recall)
Negative
20(FP)
930(TN)
Metric
0.2(Precision)
0.935(Accuracy)
위 표에서는 1000통의 메일 중 정상인 메일을 정상으로, 스팸인 메일을 스팸으로 판별한 건수는 각각 930건, 5건입니다. 1000통의 메일 중 정확하게 분류한 메일이 935통이므로 정확도는 $0.935$ 라고 할 수 있습니다. 93% 이상으로 정확하게 분류했지만 이 분류기를 좋은 분류기라고 할 수 있을까요? 오차 행렬을 다시 보면 이 모델이 얼마나 형편 없는(?) 분류기인지를 알 수 있습니다.
일단, 총 50개밖에 없는 스팸 메일 중에 무려 45통이 받은 메일함에 와있는 것을 볼 수 있습니다. 그리고 정상 메일 중 20개는 스팸 메일함에 가있어서 보지 못할 수도 있지요. 이럴 때 빛을 발하는 수치가 정밀도와 재현율입니다. 위 오차 행렬을 바탕으로 구한 분류기의 정밀도와 재현율은 다음과 같습니다.
\[\begin{aligned}
\text{Precision} &= \frac{5}{5+20} = \frac{1}{5} = 0.2 \\
\text{Recall} &= \frac{5}{5+45} = \frac{1}{10} = 0.1
\end{aligned}\]
정확도는 0.935라는 높은 수치가 나왔지만 Precision과 Recall은 이 분류기가 얼마나 성능이 떨어지는 지를 잘 보여주고 있습니다.
Precision-Recall Trade-off
어떤 것을 분류하느냐에 따라서 정밀도가 더 중요할 때도 있고, 재현율이 더 중요할 때도 있습니다. 위 스팸 메일 분류의 예시를 다시 가져와 보겠습니다. 위 분류기가 45개의 스팸 메일을 받은 편지함에 두었지만 사실 이런 것들은 손으로 직접 지워주면 됩니다. 단지 조금 귀찮을 뿐입니다. 하지만 스팸 메일함에 들어간 20개의 메일 중에서 면접 날짜나 비즈니스 미팅 날짜 확정처럼 중요한 메일이 있다고 해봅시다. 이용자는 이런 메일을 하나라도 못보면 큰일나게 됩니다. 그렇기 때문에 스팸 메일을 분류하는 분류기는 FP를 줄이는 것, 즉 정밀도를 더 중요하게 생각해야 합니다.
다른 예시로 암 환자의 X-ray 사진을 보고 분류하여 Positive이면 정밀 진단을 하고, Negative이면 무증상으로 분류하는 분류기를 만든다고 해봅시다. 이런 경우에는 어떤 수치가 더 중요해질까요? 이 분류기에서 FP로 분류된 인스턴스, 즉 암 환자가 아니지만 환자로 분류된 경우는 추후 정밀 검사를 통해서 다시 검사하면 됩니다. 하지만 FN으로 분류된 인스턴스, 즉 암 환자이지만 무증상으로 분류하면 큰일나게 됩니다. 그렇기 때문에 이런 경우는 FN를 줄이는 것, 즉 재현율을 더 중요하게 생각해야 합니다.
하지만 한 수치를 중요하게 생각하면 한 수치는 더 떨어지기 마련입니다. 예를 들어, Positive로 판별하는 기준을 빡빡하게 잡으면 정밀도가 높아집니다. 반대로 기준을 널널하게 잡으면 재현율이 늘어나게 됩니다. 스팸 메일 분류의 경우 기준을 빡빡하게 설정해서 스팸 메일로 분류되는 정상 메일이 없도록 해야하고, 암 환자 판별의 경우 기준을 널널하게 해서 정상으로 판별되는 환자가 없도록 해야 합니다.
이 수치를 설정하는 것이 바로 임계값(Threshold)입니다. 임계값을 크게 설정하면 정밀도가 올라가게 되고 작게 설정하면 재현율이 올라가게 되지요. 이런 현상을 정밀도-재현율 트레이드 오프(Precision-Recall Trade-off)라고 합니다. 어떤 분류기의 임계값에 따른 정밀도와 재현율을 그래프로 나타내면 다음과 같은 그림이 나오게 됩니다.

이미지 출처 : machinelearningaptitude.com
위 그래프 외에 재현율-정밀도 그래프를 그려 적당한 지점을 판단하기도 합니다. 아래는 재현율-정밀도 그래프의 예시입니다.

이미지 출처 : sanyamkapoor.com
F-Score
F-score(F-measure)는 정밀도와 재현율 수치를 한 번에 보기 위해서 만들어진 수치입니다. 가장 일반적으로 사용되는 수치는 $F_1 \text{-score}$ 입니다. 이 수치는 정밀도와 재현율의 조화평균으로 정리하면 아래와 같은 수식으로 나타낼 수 있습니다.
\[F_1 \text{-Score} = \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}\]
위 스팸 메일 분류기나 암 환자 판별기처럼 특정 수치가 부각되어야 할 때는 $F_1 \text{-score}$ 를 일반화한 $F_\beta \text{-score}$ 를 사용합니다. 가중치 $\beta$ 를 처리해준 것으로 정밀도가 강조되어야 할 때는 $\beta < 1$ [Ex) $F_{0.5} \text{-score}$]을 사용하고, 재현율이 강조되어야 할 때는 $\beta > 1$ [Ex) $F_2 \text{-score}$] 을 사용합니다. $F_\beta \text{-score}$ 의 수식은 아래와 같습니다.
\[F_\beta \text{-Score} = \frac{(1+\beta^2) \times \text{Precision} \times \text{Recall}}{\beta^2 \times \text{Precision} + \text{Recall}}\]
ROC Curve, AUC
분류 모델 성능 평가를 위해서 AUC(Area Under Curve) 역시 많이 사용됩니다. AUC는 말 뜻 그대로, ROC 곡선 아래의 넓이를 나타냅니다. 그렇기 때문에 AUC를 알아보기 위해서 ROC 곡선이 무엇인지 알아보겠습니다.
ROC 곡선(Receiver Operation Characteristic Curve)은 2차대전 때 통신 장비의 성능을 평가하기 위해서 나온 수치입니다. ROC곡선은 FPR(False Positive rate)을 X축으로 TPR(True Positive rate)의 그래프입니다. FPR과 TPR은 오차 행렬 내 4개의 요소를 사용한 수치이며 . 각 수치는 다음과 같이 구해집니다.
\[\begin{aligned}
\text{FPR} &= \frac{\text{FP}}{\text{FP+TN}} \\
\text{TPR} &= \frac{\text{TP}}{\text{TP+FN}} = \text{Recall}
\end{aligned}\]
FPR은 실제 Negative 클래스인 인스턴스를 얼마나 잘못 분류했는지를 나타내는 수치입니다. 그리고 TPR, 즉 재현율은 실제 Positive인 클래스인 인스턴스를 얼마나 제대로 분류했는 지를 나타내는 수치입니다.
위에서 사용했던 스팸 메일의 예를 사용해 FPR과 TPR이 어떻게 구해지는지 알아보겠습니다.
행(실제)/열(예측)
Positive
Negative
Metric
Positive
5(TP)
45(FN)
0.1(TPR)
Negative
20(FP)
930(TN)
0.02(FPR)
\[\begin{aligned}
\text{FPR} &= \frac{20}{20+930} \simeq 0.02 \\
\text{TPR} &= \frac{5}{5+45} = 0.1
\end{aligned}\]
임계값(Threshold)을 변화시키면 FPR이 변하게 됩니다. 임계값을 매우 높게 하면 Positive로 판단하는 기준이 깐깐해지기 때문에 FP가 0이 되어 FPR이 0이 됩니다. 반대로 임계값을 매우 낮게 하면 Positive로 판단하는 기준이 낮아지기 때문에 TN이 0이 되어 FPR이 1이 됩니다. 이렇게 임계값에 따라 FPR을 0부터 1까지 변화시켜가며 그에 따라 TPR이 어떻게 변화하는지를 기록한 것이 ROC 곡선입니다. 아래는 ROC 곡선의 예시입니다.

이미지 출처 : machinelearningmastery.com
낮은 FPR, 즉 임계값이 높을 때에는 성능이 좋은 분류기에서만 높은 TPR이 나오게 됩니다. 임계값이 낮아지면 어떤 분류기라도 TRP이 높아지게 되므로 FPR이 증가함에 따라 TPR은 점점 1에 가까워지게 됩니다. 이렇게 그려진 ROC 곡선의 아랫부분의 면적을 구한 것이 AUC입니다. 그래서 더 좋은 분류기는 더 높은 AUC를 가지게 되지요. 아래는 여러 분류기의 ROC커브와 AUC를 비교한 것입니다. 완전 랜덤한 분류기는 붉은 점선과 같이 ROC곡선이 그려지기 때문에 AUC가 0이 되고, 완벽한 분류기는 언제나 TPR이 1이 되므로 AUC도 1이 되는 것을 볼 수 있습니다.
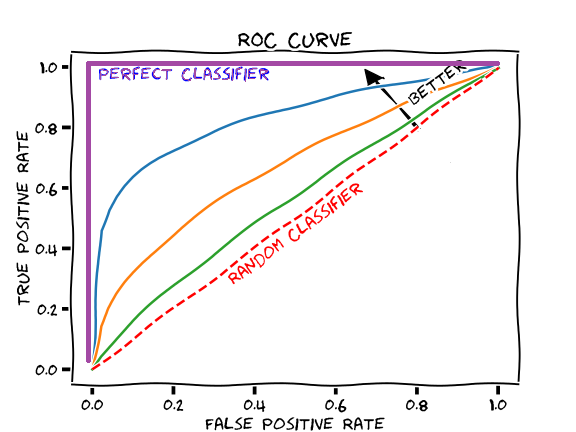
이미지 출처 : glassboxmedicine.com
좋은 평가방법이란?
머신러닝에 “공짜 점심은 없다”라는 말이 있습니다. 모든 상황에 최적화된 모델은 없다는 이야기지요. 어떤 데이터에서는 좋았던 알고리즘이 다른 데이터로 가면 성능이 떨어지는 일은 부지기수입니다. 평가방법 역시 그러합니다. AUC나 $F_1\text{-score}$ 처럼 범용적으로 사용되는 수치는 있으나 수치가 높았던 모델이 실제 데이터에서 어떤 작용을 할 지는 알 수 없습니다. 그렇기 때문에 많은 수치를 측정해보고 가장 적정한 평가방법이나 평균적으로 높게 평가되는 모델을 찾아서 하는 것이 좋은 방법이 되겠습니다.
본 포스트는 문일철 교수님의 인공지능 및 기계학습 개론 I 를 바탕으로 작성하였습니다.
Validation
가지고 있는 데이터셋을 학습 데이터와 테스트 데이터로 왜 나누어야 하는 지를 설명했을 때 나왔던 수험생을 다시 데려와 봅시다. 이전 게시물에서는 수능처럼 학생을 최종적으로 평가하기 위해서 약 20%의 테스트 데이터를 따로 빼두는 과정에 대해 설명하였습니다. 그런데 문제지만 풀다가 수능날 바로 시험을 보는 학생은 많지 않을 것입니다. 자의든 타의든 수능을 대비하기 위한 몇 번의 모의고사를 치르게 됩니다.
모의고사를 치는 이유는 무엇일까요? 수능이 끝나면 그 점수를 그대로 받아야 하는데 그 전에 자기가 부족한 부분은 어디인지, 어떤 상황에서 점수가 좋고 나쁜 지를 판단하기 위해서일 것입니다. 모의고사 결과를 보고 수능 전까지 필요한 부분을 점검하고 보완해나가게 되지요.
머신러닝 모델도 마찬가지입니다. 학습 데이터로 모델을 생성한 뒤에 중간과정 없이 테스트 데이터로 모델을 평가한다고 해봅시다. 이렇게 생성된 모델은 과적합이나 과소적합이 발생할 수 있습니다. 하지만 모델이 우리가 가지고 있는 모든 데이터를 봐버렸기 때문에 이 모델을 개선 후 다시 테스트할 수 있는 방도가 없습니다. 과적합이나 과소적합이 발생하지 않은 모델이라 하더라도 이 모델이 최선인지 더 나은 모델이 있는지 알 수 있는 방법 역시 없게 되지요.
모델에게도 테스트 데이터 전에 자신을 점검해 볼 수 있는 모의고사 같은 과정이 필요합니다. 머신러닝에서는 이를 검증(Validation)이라고 하고 검증에 사용하는 데이터셋을 검증 데이터셋(Validation dataset)이라고 합니다. 검증 데이터셋은 학습 데이터셋의 일부를 사용합니다. 다음으로 다양한 모델 검증 방법에 대해서 알아보겠습니다.
Various Validation
머신러닝 모델의 검증 방법은 크게 3가지로 나눌 수 있습니다. 첫 번째가 Holdout, 두 번째가 K-fold CV, 마지막이 LOOCV입니다. 각각에 대해 알아보도록 합시다.
Holdout
Holdout 검증은 가장 기본적인 모델 검증 방법입니다. 전체 데이터셋에서 테스트 데이터를 분리하고 남은 학습 데이터의 일부를 검증 데이터셋으로 또 분리하는 방법입니다. 즉, 전체 데이터를 3개(학습 데이터, 검증 데이터, 테스트 데이터)로 나누게 되는 것이지요. 이 방식은 가장 간단하지만 학습 데이터에 손실이 있기 때문에 데이터가 적은 경우에 사용하기 힘들고, 검증을 한 번 밖에 진행할 수 없다는 단점이 있습니다. 아래는 홀드아웃 방식을 적용했을 때 데이터가 나누어지는 방식입니다.

이미지 출처 : datavedas.com
K-fold CV
홀드아웃 방식은 학습 데이터에 손실이 있고 검증을 한 번 밖에 할 수 없다는 단점이 있었습니다. 실제로는 이를 개선하기 위한 교차검증(Cross validation, CV) 방식을 사용합니다. 교차 검증은 최소 2번 이상의 검증을 진행하므로 각 검증 결과치의 평균을 모델의 검증 결과로 사용하게 됩니다.
교차 검증의 대표적인 방식으로 K-fold 교차검증(K-fold cross validation)이 있습니다. K-fold 교차 검증은 학습 데이터를 K개로 나눈 뒤 차례대로 하나씩을 검증 데이터셋으로 활용하여 K번 검증을 진행하는 방식입니다. 이 방법도 학습 과정마다 학습 데이터에 손실이 있기는 하지만, 결국 전체 데이터를 다 볼 수 있다는 장점이 있고 검증 횟수를 늘릴 수 있다는 장점도 있습니다. 다음은 $K=5$ 인 K-fold 교차검증이 진행되는 방식을 그림으로 나타낸 것입니다. 일반적으로는 $5 \leq K \leq 11$ 범위의 $K$ 를 설정하여 사용합니다.

이미지 출처 : researchgate.net
LOOCV
LOOCV(Leave-one-out cross validation)는 K-fold 교차 검증의 극단적인 형태로, 학습 데이터셋이 극도로 작을 때 사용할 수 있는 교차검증 방법입니다. LOOCV는 오직 한 개의 인스턴스만을 검증 데이터셋으로 남겨 놓습니다(Leave-one-out). 검증 데이터가 하나이므로 학습 데이터가 총 $N$ 개라면 총 $N$ 번의 교차 검증을 진행하게 됩니다. 학습 데이터의 손실을 최소화 할 수 있지만, 샘플 데이터 수가 1000개만 되어도 총 1000번의 학습과 검증을 진행해야 하기 때문에 시간과 컴퓨팅 자원이 많이 소모된다는 단점이 있습니다. 아래는 LOOCV가 진행되는 방식을 그림으로 나타낸 것입니다.

이미지 출처 : smlee729.github.io
아래는 위 3개의 검증 방법을 비교하는 이미지입니다.
이미지 출처 : eda-ai-lab.tistory.com
Hyperparameter Optimization
검증을 통해서 과적합이 일어나는 지점을 찾는 것도 중요하지만, 성능이 좋은 모델을 찾는 것 역시 모델 검증을 해야하는 이유입니다. 더욱 성능이 좋은 모델을 만들기 위해 하이퍼파라미터 최적화를 해주어야 합니다. 하이퍼파라미터(Hyperparameter)는 학습 과정에서 모델이 알아서 바꾸는 파라미터 외에 모델을 만드는 사람이 지정하는 파라미터를 의미합니다. 대표적인 하이퍼파라미터의 예시로는 경사 하강법에서의 학습률(Learning rate), 정칙화(Regulation)의 정도를 조정하는 $\alpha$ 등이 있습니다. 모델마다 설정해주어야 하는 하이퍼파라미터가 다르기 때문에 사용하는 모델에 따라 필요한 하이퍼파라미터를 적당히 조정해주어야 합니다.
어떤 하이퍼파라미터가 최상의 결과를 낳는지 쉽게 알기 어렵고, 하이퍼파라미터의 조합에 따라서도 모델의 결과가 달라지기 때문에 검증 결과를 비교하여 최적의 하이퍼파라미터 조합을 찾아야 합니다. 최적의 하이퍼파라미터 조합을 찾는 방법은 크게 4가지로 나눌 수 있습니다.
Manual Search
말 그대로 수동(Manual)으로 하이퍼파라미터를 조정하는 방식입니다. 모델을 설계하는 사람이 경험에 의한 직관을 사용하여 최적의파라미터 조합을 설정합니다.
Grid Search
하이퍼파라미터마다 적용하고 싶은 값의 목록을 설정해둔 뒤에 그 조합을 모두 시행해보고 최적의 조합을 찾아내는 방식입니다. 직관적으로 이해하기가 쉽지만 조정할 하이퍼 파라미터가많아지면 학습 횟수가 많아지는 단점이 있습니다. 예를 들어, 학습률 $\eta = [0.001, 0.01, 0.1, 1]$ 로 4개, 정칙화 파라미터 $\alpha = [0.001, 0.01, 0.2, 3]$ 로 4개의 목록을 작성한 뒤에 각 조합에 대해 모두 학습을 수행하므로 총 $4 \times 4 = 16$ 번에 대한 학습 및 검증을 하게 됩니다.
Random Search
조정하고 싶은 하이퍼파라미터 마다 조정하고 싶은 범위를 정합니다. 실제 학습 과정에서는 범위 내에 있는 임의의 값을 설정하여 각 파라미터에 대한 조합을 정합니다. Grid search는 지정한 값에 대해서만 학습과 검증을 시도하지만 Random search는 범위 내에 있는 임의의 값에 대하여 예상치 못한 조합을 시도해볼 수 있다는 장점이 있습니다. 아래는 Grid searc h 탐색법과 Random search 탐색법을 비교할 수 있는 이미지입니다.

이미지 출처 : nanonets.com
이 3가지 탐색법외에도 베이지안 최적화(Bayesian optimization) 등 다양한 하이퍼파라미터 탐색법이 있습니다. 베이지안 최적화에 대한 자세한 정보는 수아랩(Sualab) 기술블로그에 잘 정리되어 있습니다.
Evaluation
지금부터는 검증(Validation)과 테스트(Test) 단계에서 어떤 지표를 가지고 모델을 평가할 수 있는 지에 대해서 알아보겠습니다.
Confusion Matrix
분류(Classification)에서 가장 많이 사용되는 오차 행렬(Confusion matrix)에 대해서 알아보겠습니다. 오차 행렬은 각 인스턴스의 실제 클래스와 예측 클래스의 개수를 행렬의 성분에 채워넣은 것입니다. 아래 오차 행렬에서는 각 열에 예측 클래스를, 각 행에 실제 클래스를 배치하고 있습니다. (배치는 그리는 사람에 따라 달라질 수 있습니다)

이미지 출처 : manisha-sirsat.blogspot.com
오차 행렬은 2행 2열로 구성되므로 총 4개의 성분이 있습니다. 위 오차 행렬에서 1행 1열의 성분은 True Positive(TP)이며 실제 Positive인 클래스를 Positive로 예측한 인스턴스의 개수를 나타냅니다. 1행 2열의 성분은 False Negative(FN)이며 실제 Positive인 클래스를 Negative로 예측한 인스턴스의 개수를 나타냅니다. 이 때 모델이 잘못 판단한 경우를 Type II Error라고 합니다. 2행 1열의 성분은 False Positive(FP)이며 실제 Negative인 클래스를 Positive로 예측한 인스턴스의 개수를 나타냅니다. 이 때 모델이 잘못 판단한 경우는 Type I Error라고 합니다. 마지막으로 2행 2열의 성분은 True Negative(TN)이며 실제 Negative인 클래스를 Negative로 판단한 인스턴스의 개수를 나타냅니다.
각 이름에 대해서는 “(클래스)로 예측해서 (맞은/틀린) 케이스”으로 기억하면 쉽게 기억할 수 있습니다. 예를 들어, False Positive의 경우는 “(Positive)로 예측해서 (틀린) 케이스”, True Negative는 “(Negative)로 예측해서 (맞은) 케이스” 라고 생각하면 됩니다.
스팸 메일 분류의 예를 들어 보겠습니다. 정상적인 메일을 Negative클래스, 스팸 메일을 Positive클래스라고 하면 TP는 스팸 메일을 스팸 메일로 분류한 경우, FN은 스팸 메일을 정상 메일로 분류한 경우입니다. FP는 정상 메일을 스팸 메일로 분류한 경우이며 TN은 정상적인 메일을 정상 메일로 분류한 경우입니다. 다음은 이 4개의 성분(TP, FN, FP, TN)을 활용한 정확도와 정밀도 및 재현율에 대해 알아보겠습니다.
Accuracy, Precision, Recall
가장 일반적으로 사용되는 것은 정확도(Accuracy)입니다. 정확도는 전체 데이터 중 제대로 판별한(True) 데이터의 비율로, 수치는 다음 수식을 사용하여 구할 수 있습니다.
\[\text{Accuracy} = \frac{\text{TP+TN}}{\text{TP + TN + FP + FN}}\]데이터셋에서 클래스 비율이 한쪽으로 치우쳐진 경우에는 정확도가 모델의 성능을 제대로 표현하지 못하는 경우도 있습니다. 이런 경우에 대해서는 이후 예시를 통해 알아보겠습니다. 이렇게 정확도가 모델의 제 성능을 표현하지 못하는 경우에는 정밀도와 재현율을 사용합니다. 정밀도(Precision)는 Positive로 예측한 인스턴스 중에 제대로 판별한 비율을 나타냅니다. 재현율(Recall)은 실제 클래스가 Positive인 인스턴스를 얼마나 많이 골라냈는지를 나타내는 수치이며 민감도(Sensitivity)라는 말로도 표현합니다.
\[\begin{aligned} \text{Precision} &= \frac{\text{TP}}{\text{TP + FP}} \\ \text{Recall} &= \frac{\text{TP}}{\text{TP + FN}} \end{aligned}\]위에서 사용했던 스팸 메일의 예를 들어 3개의 수치가 구해지는 과정을 알아보겠습니다. 아래는 총 1000통의 메일 중 스팸메일과 정상 메일을 분류한 예시입니다.
| 행(실제)/열(예측) | Positive | Negative | Metric |
|---|---|---|---|
| Positive | 5(TP) | 45(FN) | 0.1(Recall) |
| Negative | 20(FP) | 930(TN) | |
| Metric | 0.2(Precision) | 0.935(Accuracy) |
위 표에서는 1000통의 메일 중 정상인 메일을 정상으로, 스팸인 메일을 스팸으로 판별한 건수는 각각 930건, 5건입니다. 1000통의 메일 중 정확하게 분류한 메일이 935통이므로 정확도는 $0.935$ 라고 할 수 있습니다. 93% 이상으로 정확하게 분류했지만 이 분류기를 좋은 분류기라고 할 수 있을까요? 오차 행렬을 다시 보면 이 모델이 얼마나 형편 없는(?) 분류기인지를 알 수 있습니다.
일단, 총 50개밖에 없는 스팸 메일 중에 무려 45통이 받은 메일함에 와있는 것을 볼 수 있습니다. 그리고 정상 메일 중 20개는 스팸 메일함에 가있어서 보지 못할 수도 있지요. 이럴 때 빛을 발하는 수치가 정밀도와 재현율입니다. 위 오차 행렬을 바탕으로 구한 분류기의 정밀도와 재현율은 다음과 같습니다.
\[\begin{aligned} \text{Precision} &= \frac{5}{5+20} = \frac{1}{5} = 0.2 \\ \text{Recall} &= \frac{5}{5+45} = \frac{1}{10} = 0.1 \end{aligned}\]정확도는 0.935라는 높은 수치가 나왔지만 Precision과 Recall은 이 분류기가 얼마나 성능이 떨어지는 지를 잘 보여주고 있습니다.
Precision-Recall Trade-off
어떤 것을 분류하느냐에 따라서 정밀도가 더 중요할 때도 있고, 재현율이 더 중요할 때도 있습니다. 위 스팸 메일 분류의 예시를 다시 가져와 보겠습니다. 위 분류기가 45개의 스팸 메일을 받은 편지함에 두었지만 사실 이런 것들은 손으로 직접 지워주면 됩니다. 단지 조금 귀찮을 뿐입니다. 하지만 스팸 메일함에 들어간 20개의 메일 중에서 면접 날짜나 비즈니스 미팅 날짜 확정처럼 중요한 메일이 있다고 해봅시다. 이용자는 이런 메일을 하나라도 못보면 큰일나게 됩니다. 그렇기 때문에 스팸 메일을 분류하는 분류기는 FP를 줄이는 것, 즉 정밀도를 더 중요하게 생각해야 합니다.
다른 예시로 암 환자의 X-ray 사진을 보고 분류하여 Positive이면 정밀 진단을 하고, Negative이면 무증상으로 분류하는 분류기를 만든다고 해봅시다. 이런 경우에는 어떤 수치가 더 중요해질까요? 이 분류기에서 FP로 분류된 인스턴스, 즉 암 환자가 아니지만 환자로 분류된 경우는 추후 정밀 검사를 통해서 다시 검사하면 됩니다. 하지만 FN으로 분류된 인스턴스, 즉 암 환자이지만 무증상으로 분류하면 큰일나게 됩니다. 그렇기 때문에 이런 경우는 FN를 줄이는 것, 즉 재현율을 더 중요하게 생각해야 합니다.
하지만 한 수치를 중요하게 생각하면 한 수치는 더 떨어지기 마련입니다. 예를 들어, Positive로 판별하는 기준을 빡빡하게 잡으면 정밀도가 높아집니다. 반대로 기준을 널널하게 잡으면 재현율이 늘어나게 됩니다. 스팸 메일 분류의 경우 기준을 빡빡하게 설정해서 스팸 메일로 분류되는 정상 메일이 없도록 해야하고, 암 환자 판별의 경우 기준을 널널하게 해서 정상으로 판별되는 환자가 없도록 해야 합니다.
이 수치를 설정하는 것이 바로 임계값(Threshold)입니다. 임계값을 크게 설정하면 정밀도가 올라가게 되고 작게 설정하면 재현율이 올라가게 되지요. 이런 현상을 정밀도-재현율 트레이드 오프(Precision-Recall Trade-off)라고 합니다. 어떤 분류기의 임계값에 따른 정밀도와 재현율을 그래프로 나타내면 다음과 같은 그림이 나오게 됩니다.

이미지 출처 : machinelearningaptitude.com
위 그래프 외에 재현율-정밀도 그래프를 그려 적당한 지점을 판단하기도 합니다. 아래는 재현율-정밀도 그래프의 예시입니다.

이미지 출처 : sanyamkapoor.com
F-Score
F-score(F-measure)는 정밀도와 재현율 수치를 한 번에 보기 위해서 만들어진 수치입니다. 가장 일반적으로 사용되는 수치는 $F_1 \text{-score}$ 입니다. 이 수치는 정밀도와 재현율의 조화평균으로 정리하면 아래와 같은 수식으로 나타낼 수 있습니다.
\[F_1 \text{-Score} = \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}\]위 스팸 메일 분류기나 암 환자 판별기처럼 특정 수치가 부각되어야 할 때는 $F_1 \text{-score}$ 를 일반화한 $F_\beta \text{-score}$ 를 사용합니다. 가중치 $\beta$ 를 처리해준 것으로 정밀도가 강조되어야 할 때는 $\beta < 1$ [Ex) $F_{0.5} \text{-score}$]을 사용하고, 재현율이 강조되어야 할 때는 $\beta > 1$ [Ex) $F_2 \text{-score}$] 을 사용합니다. $F_\beta \text{-score}$ 의 수식은 아래와 같습니다.
\[F_\beta \text{-Score} = \frac{(1+\beta^2) \times \text{Precision} \times \text{Recall}}{\beta^2 \times \text{Precision} + \text{Recall}}\]ROC Curve, AUC
분류 모델 성능 평가를 위해서 AUC(Area Under Curve) 역시 많이 사용됩니다. AUC는 말 뜻 그대로, ROC 곡선 아래의 넓이를 나타냅니다. 그렇기 때문에 AUC를 알아보기 위해서 ROC 곡선이 무엇인지 알아보겠습니다.
ROC 곡선(Receiver Operation Characteristic Curve)은 2차대전 때 통신 장비의 성능을 평가하기 위해서 나온 수치입니다. ROC곡선은 FPR(False Positive rate)을 X축으로 TPR(True Positive rate)의 그래프입니다. FPR과 TPR은 오차 행렬 내 4개의 요소를 사용한 수치이며 . 각 수치는 다음과 같이 구해집니다.
\[\begin{aligned} \text{FPR} &= \frac{\text{FP}}{\text{FP+TN}} \\ \text{TPR} &= \frac{\text{TP}}{\text{TP+FN}} = \text{Recall} \end{aligned}\]FPR은 실제 Negative 클래스인 인스턴스를 얼마나 잘못 분류했는지를 나타내는 수치입니다. 그리고 TPR, 즉 재현율은 실제 Positive인 클래스인 인스턴스를 얼마나 제대로 분류했는 지를 나타내는 수치입니다.
위에서 사용했던 스팸 메일의 예를 사용해 FPR과 TPR이 어떻게 구해지는지 알아보겠습니다.
| 행(실제)/열(예측) | Positive | Negative | Metric |
|---|---|---|---|
| Positive | 5(TP) | 45(FN) | 0.1(TPR) |
| Negative | 20(FP) | 930(TN) | 0.02(FPR) |
임계값(Threshold)을 변화시키면 FPR이 변하게 됩니다. 임계값을 매우 높게 하면 Positive로 판단하는 기준이 깐깐해지기 때문에 FP가 0이 되어 FPR이 0이 됩니다. 반대로 임계값을 매우 낮게 하면 Positive로 판단하는 기준이 낮아지기 때문에 TN이 0이 되어 FPR이 1이 됩니다. 이렇게 임계값에 따라 FPR을 0부터 1까지 변화시켜가며 그에 따라 TPR이 어떻게 변화하는지를 기록한 것이 ROC 곡선입니다. 아래는 ROC 곡선의 예시입니다.

이미지 출처 : machinelearningmastery.com
낮은 FPR, 즉 임계값이 높을 때에는 성능이 좋은 분류기에서만 높은 TPR이 나오게 됩니다. 임계값이 낮아지면 어떤 분류기라도 TRP이 높아지게 되므로 FPR이 증가함에 따라 TPR은 점점 1에 가까워지게 됩니다. 이렇게 그려진 ROC 곡선의 아랫부분의 면적을 구한 것이 AUC입니다. 그래서 더 좋은 분류기는 더 높은 AUC를 가지게 되지요. 아래는 여러 분류기의 ROC커브와 AUC를 비교한 것입니다. 완전 랜덤한 분류기는 붉은 점선과 같이 ROC곡선이 그려지기 때문에 AUC가 0이 되고, 완벽한 분류기는 언제나 TPR이 1이 되므로 AUC도 1이 되는 것을 볼 수 있습니다.

이미지 출처 : glassboxmedicine.com
좋은 평가방법이란?
머신러닝에 “공짜 점심은 없다”라는 말이 있습니다. 모든 상황에 최적화된 모델은 없다는 이야기지요. 어떤 데이터에서는 좋았던 알고리즘이 다른 데이터로 가면 성능이 떨어지는 일은 부지기수입니다. 평가방법 역시 그러합니다. AUC나 $F_1\text{-score}$ 처럼 범용적으로 사용되는 수치는 있으나 수치가 높았던 모델이 실제 데이터에서 어떤 작용을 할 지는 알 수 없습니다. 그렇기 때문에 많은 수치를 측정해보고 가장 적정한 평가방법이나 평균적으로 높게 평가되는 모델을 찾아서 하는 것이 좋은 방법이 되겠습니다.

Comments